viscousな島モデルではHelpingは進化しにくい

＊MathJaxを用いて、数式入力をおこなっています。スマートフォンからの場合、PC版でアクセスしていただくと、きれいな数式をご覧になれます＊

集団がviscous「粘着的?」であるとは、生まれたパッチからの移住が100%ではない（必ずしも全員は出て行かない）ことによって、選択の対象たる相互作用が局所的（＝血縁者間で）起こるプロセスを、いいます。協力行動の進化というのは血縁者間では高まりやすいので、viscousな集団においては、helping（コストを払って、他個体を助ける行動）が有利であるような気がします。

しかしこれは実は一般にはYESとは言えないことが、島モデル上で簡単に示すことができます。（Taylor 1992, Evol. Ecol.）

まず簡単のため、無性生殖するハプロイドのオトナを\( N \)個体だけきっちり収容できるパッチが無限個ならんだ集団を考えます*1。その中で、移住前に相互作用が起こります。それによって産仔数が変化します。つまり選択はカタい（Hard Selection）とします。

具体的な相互作用による産仔数への寄与は、

（基本的な産仔数1：相互作用に関係ない産仔数）
＋（他個体からの寄与）×（その効率\( B \)）
ー（自分の協力度合）×（そのコスト\( C \)）

とします（以下参照；ただし\( B>C \)とする）。ここで、BとCの定義をちゃんとしておきましょう。

第\( i \)番目のパッチにおける、注目個体xの、基本的な産仔数\( f_i \)を、次のように定義しましょう： \begin{align*} f_i:=1+Bz_i-Cx \end{align*} ただし、\(z_i\)は、第\(i\)番目のパッチにおいて、注目個体をのぞく他の\(N-1\)個体の平均的な、協力度合です。つまり、\(B\)は、周囲の個体から助けられることによる産仔数の向上、\(C\)は協力行動の結果の自身へのリターンです。実質、たとえば\(C\)は自身の貢献 \(\beta/N\) と、投資そのものにかかるコスト\(\gamma\)の引き算という解釈もできます。\(N\)で割られているのは、皆に均等に自分の投資が配分されるからです。つまり、自分で投資することで \(\beta/N\) だけ自分からのリターンがあるが、結局はコスト \(\gamma\) が返ってくる：

\begin{align*} -C=\frac{\beta}{N}-\gamma \end{align*} と解釈します。この解釈は非常に重要です。\(C\)はあくまでも、自分が行動をおこすことによる自分へのリターン総額です。この文脈では、\(B\)は、あくまで他個体からのリターンです。1個体につき\(\beta/N\)だけ自分にゲインがあり、他個体は\(N-1\)いるので、結局\(\beta\)と\(\gamma\)とは、実は次の表式

\begin{align*} -C = \frac{\beta}{N}-\gamma,\ B = \frac{N-1}{N}\beta \end{align*}

により結びついています。*2

その後、親はいつのまにやら死に、子供たちの移住が起こります。移住は別のパッチへのものとし、移住率自体は進化しないとします。移住率を\( m \) とすると、\( (1-m) \)は元のパッチにとどまり、\( m \)は別のパッチへ移住します。*3

最後に、子どもたちは資源を巡って競争をし、N個体だけがまたオトナになれます。

こういったシンプルな生活史のもと、協力行動は進化するでしょうか？ここでは、協力行動をとらない集団\(z=0\)において、少しだけ協力するような個体xが進化できるか、解析してみましょう。

適応度\(W\)は次のようになります：

\begin{align*} W:=\frac{(1-m)(1+Bz_0-Cx)} {(1-m)(1+Bz_0^\mathrm{R}-Cz_0^\mathrm{R})+m(1+Bz-Cz)} + \frac{m(1+Bz_0-Cx)} {1+Bz-Cz} \end{align*}

ここで、\(z_0\)は、生まれたパッチにおいて注目個体自身を除く\(N-1\)個体の協力度合の平均値で、\(z_0^\mathrm{R}\)は生まれたパッチにおいて注目個体自身を含む\(N\)個体の、協力度合の平均値、そして\(z\)は集団全体での平均値です。\(z=0\)という、誰も協力行動をとっていない集団に、\(x>0\)は侵入できるのでしょうか？それを調べるためには、\(z_0\)などがどういった値なのかを知る必要があります。

集団は細分化されていて、繁殖は局所的かつ、移住は割合\(m\)として制限されているので、相互作用は血縁者間で起こる可能性があります。つまり、注目個体以外の\(N-1\)個体の中に、きょうだいが混じっている可能性があるのです。そこで、次のようなサンプリングプロセスを考えましょう。

注目個体（突然変異個体）を固定し、残りの\(N-1\)個体から1個体サンプリングし、注目個体ときょうだいかどうかを調べたところ、割合\(F\)はきょうだい\(x\)だったとします。残りの割合\( (1-F) \)は、在来型\(z=0\)であったということになります。ここでは無性生殖のハプロイドを考えているので特に、「きょうだいである＝同祖的IBDである」です。すると、

\begin{align*} z_0=Fx+(1-F)z \end{align*} であり、自身を含む平均値\(z_0^\mathrm{R}\)は、

\begin{align*} z_0^\mathrm{R}=\frac{1}{N}x+\frac{N-1}{N}z_0 \end{align*}

とわかります。特に、協力者のいない集団平均\(z=0\)でしたので、結局

\begin{align*} z_0=Fx \end{align*}

\begin{align*} z_0^\mathrm{R}=Rx \end{align*}

ただし

\begin{align*} R:=\frac{1}{N}+\frac{N-1}{N}F \end{align*}

が得られます。これはつまり、注目個体と他個体との形質上の相関が\( F \)、注目個体を含む\(N\)個体の間の相関が\(R\)であるということです。特に\(R\)は、2回のサンプリングプロセスにおいて、1回めに\(N\)個体のなかからサンプリングされた個体を一旦戻して、改めて\(N\)個体の中からサンプリングしなおした時の、IBDの確率です*4。2回めのサンプリングにおいて、確率\(1/N\)で注目個体がもう一度選ばれ、その時は確率1でIBDです。一方、残りの\( (N-1)/N \)の確率で、注目個体以外が選ばれ、その場合にはIBDの確率は\( F\)です。ということで\( R\)の表式が得られます。*5

さて、適応度が突然変異型と在来型との関数で書けたので、侵入適応度を計算しましょう。\(z=0\)は端点ですから、\(z\)よりも少しだけ大きい\(x>0\)が進化できる条件は、適応度勾配が正であること*6、すなわち

\begin{align*} \frac{\partial W(x,0)}{\partial x}{|}_{x=0}>0 \end{align*}

です。これを計算すると、

\begin{align*} FB-C-(1-m)^{2}R(B-C)>0 \end{align*} となります。ここで更に計算を進めてみましょう。世代をまたぐと\(F\)は次のような漸化式に従います：

\begin{align*} F^{\prime}= ( \frac {1} {N} + \frac {N-1} {N} F) (1-m)^{2} \end{align*}

右辺の前半のカッコ\(1/N+(N-1)F/N\)は\(R\)の定義そのものであり、現在の\(N\)個体における、本人個体を含むIBDの確率でした。つまり、それぞれの産仔数が等しいなら（定常状態ならそれは正しい）、それは分散前の子どもたちの間でのIBDの確率に等価です。ところが移住があるがために、移住・競争の後、改めて1個体サンプルして別の\(N-1\)個体のうちからもう1個体サンプルすると、IBDの確率は下がります。まず、IBDが起こるためには、両方の個体が、そのパッチで生まれた個体である必要があります。その確率が\( (1-m)^{2}\)です。その場合、もう1個体サンプルするとき、そのもう1個体と最初の1個体目とがIBDである確率は、（前の世代での分散前の子どもたちのIBDの確率が\( R\)でしたから、）\( R \)です（下図）。

f:id:lambtani:20140404035807j:image:w500

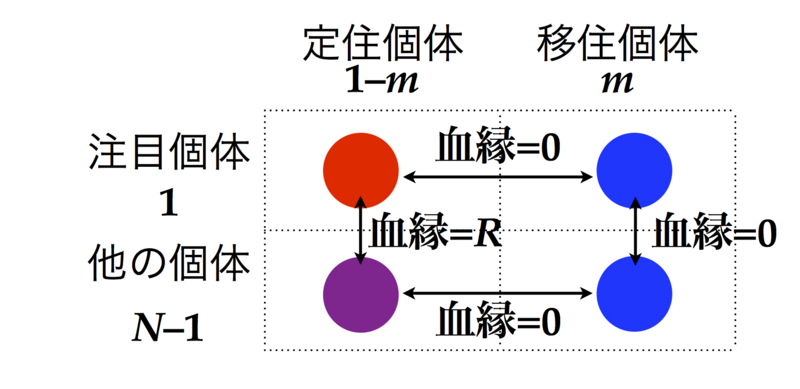
したがって、突然変異のない定常状態では、\( F=R(1-m)^{2} \)ということになります。これを代入すると、なんと、

\begin{align*} FB-C-(1-m)^{2} R(B-C) = FB-C-F(B-C)=-C(1-F) \end{align*} となり、進化条件はこれが正でしたから

\begin{align*} -C>0 \end{align*}

となるのです。そう、コストが負である、すなわち自分の協力による総合的なリターンが正でないと、「他個体を助ける」という協力行動は進化しないのです。これがキャンセリングの重要な帰結です。*7その理由は、「移動分散が抑制されていることによる、局所的な、血縁者間の資源競争の効果」と、「移動分散が抑制されていることによる、血縁者間の協力行動の結果としての産仔数の向上の効果」とが、キャンセルされてしまうからです。

βやγのことばで書いても、

\begin{align*} -C=\beta/N-\gamma>0 \end{align*} となりますので、移住が制限されていることによるviscosityのメリットはない（\( 1/N \)は自身の占める割合であり、それを超えるメリットがない）ということになります。どちらの表式でも、キャンセリングの効果がよくわかりますね。

ということで、移住が制約されているにも拘わらず、そして\( B \)がどれだけ大きくとも、viscosityだけでは、「コストを払って他個体を助ける協力行動（=Helping）」が進化しにくいということがわかってしまいました。（なお、このポストでは、「協力行動」というのは非常に広い意味で使われていて、「コストを払って他個体を助ける」のも、「公共財に投資する」のも、協力行動であるとしてごっちゃにしてしまっています。実際は、その区別をちゃんとおこなう必要があります）

そこで、友人のAntonio Rodoriguesは、